Logical reasoning is reasoning that draws conclusions based on correct understanding of relationships. Here are examples of good logical reasoning:
- Socrates was a man. All men are mortal. Therefore, Socrates was mortal.
- Abraham Lincoln was taller than his wife. His wife was taller than their 5-year-old son. Therefore, Abraham Lincoln was taller than their 5-year-old son.
- French people are thinner on average than Americans. Francoise is French and of average weight for her nationality. Susan is American and of average weight for her nationality. Therefore, Francoise is thinner than Susan.
These examples all depend on correct understandings of how elements fit into sets of elements.
Logical Fallacies
Another way to look at whether a chain of reasoning is logical is to determine whether it suffers from a logical fallacy. For example, circular reasoning is a logical fallacy. Here are examples of circular reasoning:
1.Wealthy people have made a major contribution to society. We know this because money is the reward for contributing to society.
- Telling atheists that they will go to Hell and backing that up with quotes from the Bible. Of course, the atheist doesn’t join in the assumption that a real God inspired the words of the Bible.
Circular reasoning makes an assumption which the conclusion is also based on. Often the assumption is hidden so the fallacy escapes detection. In the first example, the assumption that “Money is the reward for contribution to society,” has not been hidden. But the assumption is unwarranted because money can be inherited, stolen, or earned by fraud, etc. In the second example, the assumption that God is real is a bit more hidden.
In circular reasoning, the conclusion is only a restatement of what has been already assumed or a consequence of what has already been assumed. Circular reasoning is only one of innumerable logical fallacies. These include:
- Thinking that the converse of a true statement must also be true. For example, here’s a true statement: “If people are poor, they wear less formal clothes.” Here’s the converse: “If people wear less formal clothes, they must be poor.”
- Determining the factualness of a statement based on the source. Of course, people vary as to their trustworthiness. But when evaluating the truth of a statement, more needs to be taken into account than who said it. For many hundreds of years during the Middle Ages, the physics taught by the ancient Greek philosopher, Aristotle, was enshrined as religious doctrine. Aristotle said that the sun circles the Earth. This arrangement fit nicely with other Church doctrine, and so, doubting Aristotle’s view on the matter was deemed heretical. Famously, in the 1500’s, which was about 2,000 years after Aristotle lived, Galileo was threatened with torture unless he retracted his view that the Earth circles the sun. Turns out that attaching the name “Aristotle” to a piece of data did not guarantee its accuracy.
Many other logical fallacies beset reasoning. Finding a logical fallacy shows that a chain of reasoning is illogical.
Logical thought is not self-contradictory.
Underlying all logical reasoning is the idea that self-contradiction is not logical. This idea was first articulated by the first known writer about logic, the ancient Greek philosopher, Aristotle (384 BC-322 BC). Here is an example of self-contradiction:
- William loves all children. Phyllis is a child. William hates Phyllis.
In this example, the self-contradiction is obvious. The statement that William hates a child named “Phyllis” obviously contradicts the statement that he loves all children. However, sometimes, the self-contradiction appears as an unanticipated consequence of a chain of reasoning.
“Logical” is not the same as “factual.”
“Logical” does not mean the same as “factual,” that is, supported by empirical evidence. The statement, “French people are thinner on average than Americans” may or may not be supported by empirical evidence. Let’s say that Americans all go on crash diets, and scientists are amazed to find that, suddenly, Americans are now thinner on average than the French. The statement in #3 would still be logical, but it would include false empirical information. So, the conclusion that Francoise is thinner than Susan, though logical, would be factually false.
“Logical” describes an abstract, almost mathematical, relationship among statements. Turning to a mathematical example: 4 apples minus 1 apple equals 3 apples. One can say that we are making an empirical error of fact by calling these things apples:
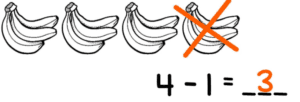
But the math (4-1= 3) is impeccable. Logic is similar to math. Logical thought reflects only correct relationships. To say that something is logical is not to say that it reflects correct empirical facts.
However, people frequently say that something is not logical when they mean it relies on incorrect facts. This is a misuse of the concept of logic. Let’s take the example of little Sarah rushing to her father and screaming, “Daddy, I just saw a ghost!” Her father might take Sarah in his arms and try to comfort her by saying, “Now, Sarah, it’s just not logical to think that there are ghosts.” Putting aside the issue of whether this is a helpful response, has Dad used the word “logical” correctly? No. At this writing (2019), there is no proven scientific theory from which one could follow a chain of reasoning to conclude that ghosts don’t exist. Mainstream physics theories do not address things that are not physical or material. And ghosts, if they exist, might be something other than physical or material. At this time, the existence or non-existence of ghosts is not addressed by science and is purely an empirical issue.
Yet, many people conflate “logical” with “empirically correct” or “scientific.” We tend not to differentiate between our assumptions regarding reality and our ability to use logic. In the above example, Dad reasoned something like this:
- Ghosts don’t exist. We can only see things that exist. Sarah says she saw a ghost. Sarah is being illogical.
It would be correct to think that Sarah was being illogical only if the statement, “Ghosts don’t exist” is empirically proven. But this is an unproven assumption. Dad would have been more accurate if he had said, “I don’t think ghosts are real.” And, his daughter’s confidence in her ability to reason logically might have been spared.
Illogic is easier to show than logic.
How does one show that a chain of reasoning is logical? One can point out that it accords with proper relationships, doesn’t suffer from any known logical fallacy, and it doesn’t result in self-contradiction. So, it’s not illogical. Does that mean that the reasoning is logical? There really isn’t a test for logic other than our intuition as to what seems logical. We can eliminate sources of illogic and only hope that we haven’t missed one.
