« Back to Glossary Index

This article starts with the nature of wave equations in classical physics and moves into a brief description of the Schrodinger Wave Equation and the wave function. This encyclopedia also includes separate articles on the Schrodinger Wave Equation and the wave function.

Wave equations in classical physics are equations which describe waves. Imagine a water wave rolling onto the beach. An equation might tell us, for any one moment, how to calculate the force of the wave when it hits an unwary child, based on the height of the wave (amplitude). We could use the same equation a moment later to describe its new force and height. And so on, moment to moment. Such an equation would tell us how the wave’s height and force change over time.

Physicists would say that they use wave equations to calculate how a wave “evolves.” Feed some numbers describing these properties at one moment of time into the equation, do some calculations using the equation, and out come values for these properties at a later moment in time.

To the right is an example of an equation for the height and force of a water wave. Without going into any detail as to the meaning of the symbols (other than h = height), here’s what this equation is saying: take the height and some other measurements of the wave and do some mathematical manipulations, and you’ll get a measure of the wave’s force.

This equation is for deep ocean waves. It was written by a professor at the University of California at San Diego in a set of exercises for applying physics to surfing. A physicist looking at the form of this equation would be able to see that it is an equation for waves.

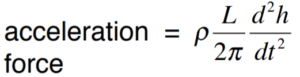
Forms of Equations

Equations which describe different things take different forms. Usually, the first form that students learn in school is equations for straight lines.

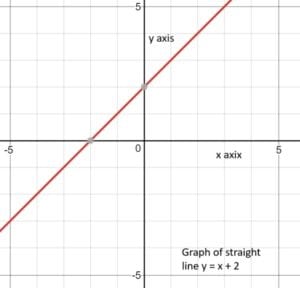For example, y= x¹ + 2 is the equation that allows us to graph the straight line in the accompanying diagram. A simpler way to write this equation is y= x + 2. This equation tells us to feed in a number for x and out comes the number y. If we input x = 0, we output y = 2. Input a variety of values for x, and you get the corresponding values of y. The accompanying graph shows how these x and y values can be plotted as a straight (red) line.

Any equation in which there is only one unknown, x, and x is raised only to the first power, as in this example, describes a straight line. Here are some other examples of equations for straight lines:

y = 2x + 4               y = -3x – 4                  y = 2.7x – 9.3

A physicist or mathematician looking at them would say, “These are equations for straight lines.”

 

 

 

Looking only at the form of the equation without going into any further detail, here’s an equation for a sphere: (x-h)² + (y-j)² + (z-k)² = r². This equation differs from the form of an equation for a straight line in two ways: (1) It includes the power of 2 (squaring) and (2) It includes three unknown variables (x, y, z) rather than just one. A mathematician who looks at an equation like                   (x-1)² + (y-2)² + (z-1)² = r²  would say, “That’s an equation for a sphere.”

The accompanying image graphs the equation (x-1)² + (y-2)² + (z-1)² = r² , an equation for a sphere.

Equations for straight lines and spheres describe geometric shapes. Equations can also describe the behavior of moving, evolving things as in an equation for a wave. Here’s another example of an equation that describes a moving, evolving thing. It’s an equation with which you’re undoubtedly familiar: e = mc². This equation tells us how much energy (e) is released when mass (m) converts to energy. Take the amount of mass, multiply times the speed of light (c) squared, and voilà, that’s how much energy would be released if all the mass were converted to energy. A more detailed version of this equation can be used to describe, for example, how much energy is released by plutonium due to a chain reaction in a nuclear bomb explosion.

Schrodinger’s Wave Equation

Why is Schrodinger’s Equation called a “wave equation”? Its form is that of a wave equation. Scientists looking at the equation, without knowing what it describes, would be able to guess that it describes a wave. That the equation is in the form of a wave equation is no accident, as its famous history demonstrates.

In 1926, Schrodinger gave a lecture in which he said that the electron inside an atom moves like a wave. In fact, Schrodinger rejected the idea of particles altogether. To him, matter was made of waves. A physicist in the audience, Peter Debye, was skeptical. He asked, if the electron is a wave, where is the wave equation that describes it? Schrodinger took this as a challenge.

Shortly after the lecture, Schrodinger vacationed for 2 ½ weeks in the Swiss Alps. Rather than taking his wife, he took along a girlfriend, whose name remains lost to history. During the vacation, in addition to anything else that happened, he also developed his famous equation. It is called the Schrodinger Wave Equation because its form is that of a wave equation.

 

Quantum Waves 

What is a wave? It’s a pattern of movement that propagates itself through a medium. A motion in one particle instigates the same motion in neighboring particles. A wave that travels through the crowd in a football stadium is a good metaphor for a wave in physics. Each person stands and inspires his/her neighbor to stand. The motion ripples through the crowd.

In the case of a physical wave, the motion naturally self-propagates from one particle to the next. For example, sound is a pattern of compressions and rarifications (dispersals) of air molecules, propagating rhythmically through the medium of air. Another example is waves in the ocean, where the up and down motion of water molecules manage to also travel sideways, pushing their neighbors into the same pattern of motion.

One might ask, what is the medium that the electron wave is propagating through while inside the atom? This is a central question of quantum physics which is still being debated. For a discussion, see quantum physics interpretations.

Schrodinger’s Wave Equation Versus the Wave Function

The solution to Schrodinger’s Wave Equation is not a number as is the case of an equation for a line. In a line equation, one feeds in x and gets the number y. Instead, the solution to Schrodinger’s Wave Equation is another equation or a set of equations. The equations which solve Schrodinger’s are called “wave functions.” Here, “function” means a particular kind of equation. So, the Schrodinger Wave Equation specifies a wave function. And the wave function describes the wave-like properties of quantum particles. Specifically, the wave function tells us the probabilities that the particle will be in a one position rather than another or have one energy level rather than another.

See wave function and the Schrodinger Wave Equation for further information.