« Back to Glossary Index

The term “superposition” is used in both classical physics and quantum physics. In this article, “superposition” is addressed primarily as a quantum phenomenon. Classical superposition is touched on briefly at the beginning and in its own article superposition, classical waves.

Superposition of Classical Waves 

The term “superposition” was first used in classical physics. In classical physics, waves are said to be in a superposition when they meet and run through each other. When the two waves run through each other, they are on top of each other. This is called a “superposition.” When in a superposition, they can change each other in a number of ways. But upon parting, amazingly, they return to their original forms.

In the accompanying video, two waves approach each other from opposite directions. These might be, for example, waves in water or sound waves in the air. Upon meeting, they form a superposition–two waves superimposed on top of each other. In this case, they amplify their heights—the heights of the two waves add together to make a taller wave. I find the next bit quite magical: once they’ve passed each other, they emerge unscathed as if nothing had happened. They return to their original heights. (To run the video in slow motion, perhaps at .5 speed, click on the Settings icon (a gear or cogwheel), then click Speed, then .25 (quarter-speed) or .5 (half-speed).)

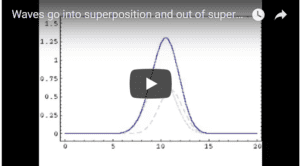
In this video the waves are perfectly in sync (technically “in phase”). That is, both waves go up into crests and go down into troughs at exactly the same moment. As noted, in this situation, they amplify each other before parting ways.

But, of course, waves might meet that are out of phase. That is, they might crest at different times. If they were perfectly out of phase so that one crested exactly at the moment that the other bottomed out into a trough, they would cancel each other. Upon meeting, the water would go flat. In this superposition, it would appear that there were no waves at all. Then, once the waves had passed each other, they would emerge again, in the same forms that they had assumed prior to meeting–just as if nothing had happened. Click for more information about classical superpositions.

Quantum Superposition

Quantum mechanics took the term “superposition” to describe a quantum state analogous to classical superpositions but even more magical. The quantum state of Schrodinger’s cat is called a “superposition.” The cat ends up in a state of being both dead and alive; it’s in a superposition of being both dead and alive. Sometimes, people say that

an electron is in a superposition of being in more than one place at the same time. (See image to right and click on it to watch the video). Or it’s in a superposition of spinning both clockwise and counter-clockwise at the same time. No, I’ve not seen an attempt to make a still image of that! But below is a video of an atom in a superposition of being in an excited state (when it enlarges) and a less excited state (when it shrinks). To watch the animation, click here. 

To say that a quantum particle is in more than one state at the same time is a quick and dirty way to describe a “superposition.” And it gets across the general idea. But it’s not really accurate, and we can’t wrap our minds around it. How can an electron spin both clockwise and counterclockwise at the same time? How can a cat be both dead and alive? What is really going on?

Example of a Quantum Superposition

To explain what’s really going on, consider an experiment in which an electron is trapped in a box. The electron is magnetic and is repelled by the magnets which surround it on all sides—this is an electron trap. The box also holds an electron detection screen. This might be a screen treated with chemical phosphor. A tiny pixel of phosphor in the screen lights up when an electron interacts with it.

Let’s say that experimenters would like to calculate where the electron is. They calculate the behavior of the electron in the box using an equation derived from the Schrodinger Wave Equation. This derived equation is called a “wave function.” (A function is a common type of equation, often referred to in algebra.)

If the electron were like a baseball, the wave function would tell us where the electron is at any moment in time. Staying with the baseball, if a batter were to hit it with a known amount of force, physicists could calculate the position of the baseball at any particular moment in time. They would apply the laws of force originally developed by Isaac Newton in the 1600’s. Every moment, the baseball would occupy a different position in spacetime. When it was caught, it would be in spacetime too. It never disappears from spacetime. This is not the way quantum particles behave.

The wave function derived from Schrodinger’s Equation doesn’t tell us where the electron is. Nor does it tell us that the electron is in many places at the same time. Instead, the wave function tells us a set of probabilities as to where the electron will appear if it is detected. The wave function assigns a probability to each spacetime position in which the electron could possibly be detected. While the experimenters would like to know where in the box the electron is at any one moment, the best that they can do is calculate the probabilities of where it will be detected.

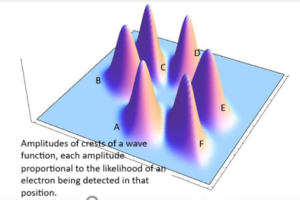
Now we can return to the term “superposition.” The electron is in a superposition until detected. When not detected, it isn’t considered to be in position in spacetime. Rather, it’s in a quantum superposition of probabilities. Physicists describe the electron as being in a “probability state” or a “probability wave” or an “electron cloud.” This superposition can be described mathematically. But it cannot be described as an object or energy in a particular position in spacetime or even in a group of positions in spacetime.

The accompanying image is an imaginary graph of the probabilities as to where the electron might be detected in the magnetic box. This is a graph of a superposition. Each wave peak represents a probability of an experimental result rather than representing the position of a physical object or energy. According to this graph, the electron might be found in six different positions when it is detected (A, B, C, D, E, F). In this case, due to the particular set-up of the magnets, the electron has an equal probability of being detected as a particle in each position. This is indicated by the equal heights of the wave peaks. This graph shows what’s going on in “Quantumland.”

Quantumland

This explanation of “superposition,” that it is a state which is not in spacetime, comes from the Transactional Interpretation of quantum mechanics. In this

interpretation, quantum particles are in Quantumland, and Quantumland is a level of reality underlying spacetime. The wave function, not Newton’s Laws, are used to calculate the wavy, apparently insubstantial, possibilities of where the electron will be detected.

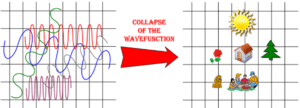
While Quantumland may seem insubstantial, it determines what happens in spacetime. True, Quantumland only sets the probabilities, but the behavior of quantum particles which are detected in spacetime must conform with the probabilities.

 

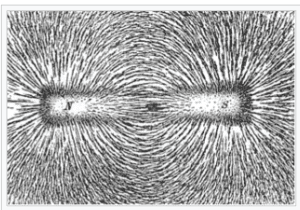
This situation is analogous to the school experiment where iron filings sit on a piece of paper with a magnet under the paper. Shake the paper and the filings arrange themselves nicely into curved lines. The filings, real bits of matter, are being pushed around by a field that isn’t even visible. The Quantumland inhabitants, which appear to be only mathematical probabilities, calculate the behavior of a real object, an electron. In the Transactional Interpretation, the explanation for this is that Quantumland is a wavy level of reality that underlies spacetime and determines the behavior of physical objects in it.

Those who favor the Information Theory approach would say that, upon detection, information has been irreversibly created. The position of the electron is no longer insubstantial probabilities; it takes definite form within spacetime. When the electron interacts with the phosphor pixel in the detection screen, the universe has changed. The superposition of probabilities has collapsed into an electron, and the electron has caused a change in the phosphor of the detection screen. This change is a change to the information of the physical universe. According to Information Theory, this is the physical meaning of the collapse of the superposition (as described mathematically by the wave function) to a particular position in spacetime.

Superpositions in the Copenhagen Interpretation

The original interpretation of quantum mechanics, the Copenhagen Interpretation, however, interprets “superposition” differently. This interpretation was developed in the 1920’s and 30’s by the founders of the field of quantum mechanics. Like the Transactional Interpretation and most other interpretations of quantum mechanics, it derives the wave function from the Schrodinger Equation to describe the superposition. But it’s mum on the issue as to whether there is any reality to the wavy probabilities calculated by the wave function. It declines to address the issue, describing the question as “unscientific.” This is due to a philosophy that was current at the time that the Copenhagen Interpretation was developed, a philosophy of science called “logical positivism.” According to logical positivism, science should address only those things which can be measured and should stay clear of everything else. In summary, in the Copenhagen Interpretation, the physical nature of quantum superpositions cannot be described. They are a set of probabilities calculated by the wave function, and nothing more can be said about superpositions.

Other Interpretations of “Superposition” 

About 15 interpretations of quantum mechanics have been developed to describe the physical nature of quantum behavior. Most interpretations stick to

identical mathematical formulations, though some add to or slightly vary the equations. At one end is the de Broglie-Bohm Interpretation: A physical wave, created by a previously unknown force, guides a quantum particle to its position in spacetime. The electron is like a surfer pushed along by the wave that it rides. The wave is always present and the particle is always present. Thus, the electron has both wave and particle qualities. Unlike the Copenhagen or Transactional Interpretations, the wave doesn’t collapse and  become a particle.

At the other end of the range of interpretations is the Many Worlds Interpretation: Every wavy possibility manifests as a particle in a different universe. The wave function calculates the probability of the electron being detected in every possible position on the detection screen. The universe in which the experiment is done splits into innumerable universes, each with the electron assuming a different position on the detection screen. In each universe the experimenters have been duplicated and are present. They record the results of the experiment as it appears in their universe, unaware of the positions that the electron has assumed in other universes.

The Many Worlds Interpretation has the advantage of assigning physical meaning to the wave function. It doesn’t require adding a new, insubstantial layer of reality. It keeps everything very physically real. The meaning of the probabilities calculated by the wave function is, however, problematic. Despite this issue and the fantastical idea of hatching an infinite number of universes every time a quantum particle “makes a choice,” the Many Worlds Interpretation is becoming quite popular among physicists (as of this writing in 2019).

For other interpretations of the meaning of the quantum superposition see interpretations of quantum mechanics.