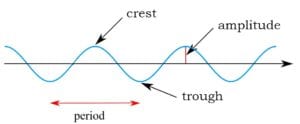
The amplitude of a wave is its height, that is, half the distance from trough to crest. Amplitude can be measured for water waves, sound waves traveling through air, or for any other type of wave traveling through a gas or liquid. Even waves traveling through a solid have an amplitude, as in waves shaking the Earth due to an earthquake.
Amplitude of Material Waves Determines Energy
For waves that require a material medium, like water waves or sound waves, the amplitude determines the amount of energy of the wave. More precisely, the energy with which a wave hits is equal to the amplitude squared. So, if you were standing on the beach and were hit by a water wave one foot tall, little would happen. But if it were two feet tall, the wave would have four times the impact (2 squared = 4). If it were four feet tall, it would have 16 times the impact (4 squared = 16). If the wave were as tall as a tsunami…well, you know what would happen then.
This relationship between amplitude and energy holds true for any wave that requires a material medium. These are classical waves; they can be described by Newton’s Laws of Motion. However, the relationship between amplitude and energy does not hold true for quantum waves. Quantum waves do not require a material medium and do not follow Newton’s Laws of Motion. Rather, they follow the laws of the quantum world.
Amplitudes of Quantum Waves
Quantum particles have properties of both waves and particles. When considered as waves, they have amplitude. However, the amplitude of a quantum wave does not determine the wave’s energy. The energy of a quantum wave is proportional to its frequency rather than to its amplitude.
The properties of quantum entities are less straightforward than the properties of everyday objects like tables and chairs. Quantum waves have amplitude in the sense that their amplitude can be calculated. No one has ever seen a quantum wave, nor has seen if they actually have height. According to the original interpretation, that is, the Copenhagen Interpretation of quantum physics, it makes no sense to even try to visualize the height of a quantum wave. While the amplitude of a quantum wave can be calculated, it is granted no physical reality.
Amplitudes of Quantum Waves Determine Probabilities
Instead of determining energy level, the amplitude of a quantum wave determines probabilities. For example, where wave amplitudes are calculated as higher, the associated particle is more likely to be detected. Specifically, the likelihood of detecting the particle in a particular position is equal to the square of the amplitude in that location.
The amplitude of a quantum wave is also called the “probability amplitude.” When the probability amplitude is squared in order to calculate actual probabilities, it is called the “probability density.” 1
A key feature of the quantum world is that the behavior of quantum particles is not deterministic as in the everyday world of tables and chairs. The behavior of quantum particles is, instead, probabilistic.
It may seem surprising that the amplitude of quantum waves has a different physical implication than the amplitude of classical waves that create ripples in matter. However, the term “wave” is used in quantum physics only on analogy with the classical waves that we see in everyday life; quantum waves are not at all the same beast as everyday waves.
Quantum Amplitudes Expressed with Imaginary Numbers
Often quantum waves have amplitudes that must be expressed with imaginary numbers.
A note to define imaginary, real, and complex numbers (skip if not needed): An imaginary number is one that includes the square root of -1, written √(-1). What number multiplied by itself, that is, squared, equals -1 ? No ordinary number fits the bill. It’s an imaginary number. Nevertheless, we can write it √(-1) .
√(-1) can also be written as i (for “imaginary” or “impossible”). An entire set of imaginary numbers can be created by multiplying i times a regular number, for example: 3i 4 ½ i -7.35 i
Imaginary numbers have proved very useful in both math and physics.
Often, when we describe the physical universe, we use ordinary numbers, called “real numbers.” These are all the numbers that could be used to express distances measured by a ruler:
0, 1, 4 ½, 7.9543… -1, -2 ¾, -5.6983…
A real number can be combined with an imaginary number, for example:
3 + i -14 + 4i 5 – 2.7i
The combination of both real and imaginary numbers is called a “complex number.”
Back to amplitudes. Often the amplitude of a quantum wave is expressed as a complex number, that is, it has both a real part and an imaginary part. When the amplitude is used to calculate the probability of detecting an electron or other particle in a particular position, the amplitude is squared.
Most interpretations of quantum mechanics do not give physical meaning to the imaginary numbers that characterize quantum wave amplitudes. The appearance of imaginary numbers arising from the Schrodinger Equation is considered just one more unaccountably odd aspect of quantum mechanics. However, the Transactional Interpretation assigns special physical meaning to the imaginary numbers in quantum wave amplitudes. Quantum wave amplitudes are considered to exist in a physical reality outside of spacetime but which determines behavior of particles in spacetime. For more information, see Transactional Interpretation.
Footnotes
