Month: March 2019

March 14, 2019

Why does the Born Rule predict quantum probabilities?

There’s both a mathematical explanation and an explanation based on the nature of reality.

First, the mathematical explanation: Let’s take the example of the Double Slit Experiment. A laser shoots photons one-at-a-time through the two slits of a

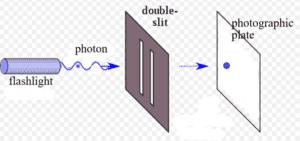
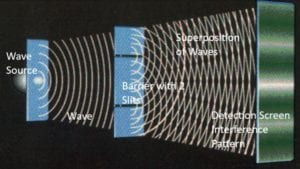
Double Slit Experiment shooting one photon at a time. [Image source: modification of https://en.wikipedia.org/wiki/Double-slit_experiment]

screen towards a photographic plate. The wave function is the equation that describes the behavior of the

Waves pass through two slits and create an interference pattern. [Image source: Dan Hooper, Fermilab http://saturdaymorningphysics.fnal.gov/wp-content/uploads/2017/02/Hooper-II-2017.pdf p. 36]

photon. The amplitudes calculated for the wave by the wave function are proportional to the probability of the photon being detected in any particular position on the photographic plate.

The mathematical expressions for the wave amplitudes often include complex numbers (numbers that include the square root of negative 1). We cannot visualize such a number because what number multiplied times itself equals negative 1? There is no such number. We label this non-number as i and just don’t try to imagine what amount i really represents. Even though i does not describe anything that we’re familiar with in the physical universe, both mathematicians and physicists have found it useful to work equations which include i, that is, complex numbers.

Amplitude is a key property of waves. The horizontal axis is time. [Image source: modification of Kraaiennest – CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=4038226. Retrieved Sept. 21, 2017.]

While neither water waves nor sound waves nor any other wave that we might observe in the physical universe have amplitudes that can be measured by complex numbers, the wave function often calculates complex number amplitudes for quantum waves. This is a clue that quantum waves do not operate in the spacetime of our physical universe. In the Copenhagen Interpretation, the original and conventional interpretation of quantum mechanics, it’s not clear where they operate. The status of their reality is an enigma wrapped in a mystery. A bit later in this answer, another interpretation will provide more information on the issue.

But returning to the wave function in the Copenhagen Interpretation. Max Born (1882-1970) was the quantum physicist who first realized that the amplitude of the quantum wave predicts the probability of detecting a particle in a particular position. But this creates a problem. What if the amplitude includes a complex number?

A probability cannot be expressed using complex numbers. Probabilities are expressed as positive numbers ranging from 0% to 100%. That is, we can say that there’s a 50% chance when tossing a coin of getting heads. Or a 0% chance that every moment of the day will be fun. And a 100% chance that a human being will eventually die. But to say that the chances of an event are the square root of negative 1 makes no sense.

Max Born (1882-1970), developer of the Born Rule. [Image source: Public Domain, https://en.wikipedia.org/wiki/Max_Born]

Born solved the problem by multiplying the amplitude of the wave by its complex conjugate. This squares the square root of negative 1, yielding simply negative 1. The result is probabilities calculated by the wave function are quite nice. They range from 0% to 100%.

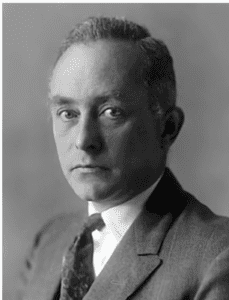
This calculation is the Born Rule. Experimental results show that the Born Rule is accurate in calculating quantum behavior. So, not only does the rule cancel out the troublesome complex numbers, it accords with empirical results. The Born Rule is an integral part of the Copenhagen Interpretation.

However, the Born Rule does not explain what is happening in the physical universe that requires that we multiply the wave amplitude by its complex conjugate. Nor does any other part of the Copenhagen Interpretation provide such an explanation. The Transactional Interpretation does. While it would be too lengthy to fully explain this interpretation here, an example gives a taste:

Let’s say take a look again at the Double Slit Experiment with a laser emitting a single photon towards a photographic plate. Until it arrives at the photographic plate, it’s a quantum wave that physicists can calculate a wave function for. The wave function identifies the possible positions where the quantum wave could deposit its energy on the photographic plate. So far, this is like the Copenhagen Interpretation. But the Transactional Interpretation adds something new. It says that if the photon is to land on the photographic plate, an electron in the plate must take action to absorb it. Electrons in the plate must send out their own waves. When the emitting wave and the receiving wave interact, the photon transfers energy to the electron, and takes its place in physical reality at a position on the plate.

The wave function of the absorbing electron in the plate has an amplitude that fits well with the amplitude of the photon: it’s the complex conjugate of the photon’s amplitude.

But why multiply the two amplitudes? This is how we find the probability of two events occurring, in this case both the photon heading towards a particular position on the plate and an electron in that position absorbing it. When we calculate the probability of any two events, we multiply the two probabilities. For example, the chances of a baby being born a girl with brown eyes is: 1) the probability of being a girl (about 48%) times (2) the probability any baby having brown eyes (about 80%). We multiply 48% times 80% and get 38%. There’s a 38% chance that a baby born anywhere in the world will be a girl with brown eyes.

The emitting wave and the absorbing wave have to interact if the photon is to land in any particular position. We multiply the probability of the photon landing in a particular position (the complex number describing the amplitude) times the amplitude of the receiving wave at that position on the plate (the complex conjugate).

The Transactional Interpretation is based on Absorber Theory developed by Richard Feynman and John Wheeler in the late 1930’s. It was fully developed as an interpretation of quantum mechanics by John Cramer in the 1980’s and further developed by Ruth E. Kastner. Kastner has written technical papers on the Transactional Interpretation and also a book for laypeople, Understanding Our Unseen Reality. I highly recommend the book because it provides a coherent and understandable explanation of the physical meaning quantum mechanics.

March 13, 2019

How do we know a quantum particle is in a superposition if detecting the particle will destroy the superposition?

It’s not possible to KNOW that the particle is in a superposition of states since we can’t observe the superposition. The superposition idea is trying to explain what must be happening in the real world given that Schrodinger’s Wave Equation works. Schrodinger’s Wave Equation (and later upgrades like the equations of Quantum Electrodynamics) are very successful at predicting the results of quantum physics experiments. The Copenhagen Interpretation, the original interpretation of Schrodinger’s Wave Equation, describes the reality underlying the equation as a superposition.

Quantum physicists are in a situation similar to chemists before atoms could be observed with powerful microscopes. (See this article for information on our current ability to observe atoms.) Chemists predicted the results of their experiments on the assumption that atoms exist. They used atomic behavior in their calculations very successfully. Yet, for a century, from the 1800’s into the 1900’s, they had no hope of observing atoms. Some might have said that even, in principle, observation would be impossible. Similarly, many quantum physicists describe the state of quantum particles prior to detection as a superposition because doing so helps them to understand what is going on. They probably have even less hope of detecting a superposition than did chemists regarding observing an atom.

However, interestingly, I just ran across this article on a proposed 2018 experiment that may help them take a peek into the world of the superposition.

Alternatives to the Superposition Idea

The concept of the superposition is part of the Copenhagen Interpretation of quantum mechanics. But there are other explanations, for example, the de Broglie-Bohmian Interpretation, the Many Worlds interpretation, the Transactional Interpretation, and many others. Many don’t require the superposition idea.

The Superposition Idea Is Workable

The superposition idea, whether it will survive in the long run, is useful. Take the example of a photon of sunlight in photosynthesis. Plants are able to use the red photons from the sun. Red photons zip through the cells of a leaf to the “reaction center” where they provide the energy for photosynthesis, that is, the production of sugars.

The trouble is that, once absorbed by a molecule of chlorophyll, the photon must find its way through a maze of cells to find the reaction center, where it will contribute its energy. If the photon used the ordinary strategy of wandering through the maze, its energy would be lost long before it reached the reaction center. But, in fact, biologists have found that plants are able to use almost every red photon for sugar production. How?

Quantum equations to the rescue! Scientists can use quantum equations to describe what the photon actually does, which is different from wandering through a maze of cells. But what is the photon actually doing physically? The Copenhagen Interpretation is that while in a superposition, the photon is experiencing a superposition of all paths. (Richard Feynman would say that it is traveling all possible paths.) Then, it enters physical reality having selected the fastest path. Here is a 4-minute video describing this:

And here is an academic paper which gives a more technical description: Quantum mechanics explains efficiency of photosynthesis

One way to look at this is that the equations show that the photon is in a superposition. However, that’s only one look at it, the Copenhagen Interpretation way. The same equations appear in other interpretations of quantum physics and predict the same results for the red photon. There’s lots of information about these interpretations in books and on the web, starting with this Wikipedia article: Interpretations of quantum mechanics – Wikipedia

March 9, 2019

What are some good online resources that can help me understand physics better?

The Physics Classroom and Khan Academy both have excellent free on-line courses on physics, starting from the beginning. They’re step-by-step and give practice problems. On Khan Academy, if you sign in, it will keep track of your progress. It also gives “awards” like badges for good progress. Both websites are excellent. Khan Academy is a little more interactive. I have used both. To really gain understanding and certainty, I’ve done lessons on the same subject on both websites.

When I didn’t understand something in a particular lesson, I found videos on Youtube. I typed the subject into the Youtube search bar, for example, “inertia.” Then, I just started watching videos until I finally got it.

It’s important to understand all the jargon as it comes up. When terms came up I wasn’t sure of, like “mass,” I watched Youtube videos on the subject and/or googled the physics meaning. When googling, I often asked for images. Finding visuals really helps.

I’m writing definitions of physics terms in an on-line encyclopedia. It focuses on quantum physics, but many of the terms, like acceleration, are shared with classical physics. Classical physics is the first physics that you learn on websites like the PhysicsClassroom and KhanAcademy.org.

March 7, 2019

How do I get started in learning quantum mechanics?

Videos on the Youtube channel “Looking Glass Universe” provide the clearest intro to quantum mechanics that I’ve found. They don’t require math nor a prior knowledge of physics, and they take it slow. However, they really get you into the midst of quantum mechanics. It’s not a light once-over. Of course, start with #1 and take them in sequence. They’re each about 10 minutes and there are about 14 of them.

For more of a light once-over, documentaries hosted by Brian Greene on Youtube are excellent. He’s a quantum physicist and a noted science writer.

Good beginning book on quantum mechanics is Fields of Color by Rodney Brooks.

I’m assuming here that you already know the basics of Newtonian physics. If not, study these first. The Physics Classroom is an excellent free on-line course on Newtonian physics. It’s step-by-step and gives practice problems. Khan Academy also has excellent free lessons on Newtonian physics.

Whenever I didn’t understand something in a particular video or book on quantum mechanics, I found videos or on-line articles about that particular thing until I had more understanding of it.

I’m writing definitions of quantum physics jargon for people who are interested in quantum physics but don’t want to dive into the math of it. It’s the definitions and the illustrations and examples that I wish I had when I was first watching these videos and floundering around. I’m hoping that it will help others.